티스토리 뷰
트리
트리란 노드와 간선으로 이루어진 자료구조로 부모노드에서 자식노드로 향하는 계층 구조를 이루고 있다.
그래프의 한 종류이지만 트리는 사이클이 존재하지 않고 노드간 연결 경로는 부모에서 자식으로 오직 하나 뿐이라는 특징이 있다.
트리에는 이진트리, 이진탐색트리, 완전이진트리가 존재한다.
선형구조로는 계층 구조를 사용하지 못하기에 트리라는 자료구조를 사용한다.
대표적인 사용사례가 DB의 인덱스 페이지이다.
책의 목차와 같은 계층 구조를 통해 데이터의 빠른 접근을 보장한다.
트리의 정의
- 하나의 루트 노드가 반드시 존재
- 루트 노드를 제외한 모든 노드는 부모노드를 갖음
- 모든 노드는 0개 이상의 자식 노드를 가질 수 있음
- 사이클이 존재하지 않음
- 노드의 갯수가 N이면, 간선의 수는 N-1
트리는 방향그래프? 무방향 그래프?
그래프 이론에서 트리는 노드간 연결에만 초점을 두어 무방향 그래프로 취급 받지만,
자료구조에서는 부모노드에서 자식노드로의 방향이 존재하는 방향 그래프로 취급한다.
트리의 시간복잡도
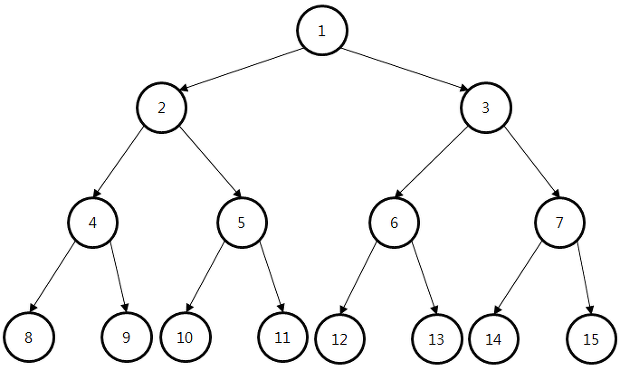
트리의 높이가 h일 때, 노드의 갯수 N=(2^h)-1을 따른다.
트리 자료구조에서 리프노드에 도달하는 탐색 횟수는 트리의 높이와 같으므로 h=log(N+1) ≈ logN을 따르게 된다.
따라서 트리 자료구조의 조회 시간복잡도는 O(logN)이다.
O(logN)은 굉장히 빠른 편에 속하는 시간복잡도이다.
하지만 트리가 모두 O(logN)의 시간복잡도를 보이는 것은 아니다.
트리가 평균 O(logN)의 시간복잡도를 보이기 위해서는 균형을 이루는 것이 중요하다.
앞으로 알아볼 다양한 트리를 통해 알아보자.
이진트리
모든 노드가 최대 2개의 자식 노드를 가지는 트리로 왼쪽 자식노드와 오른쪽 자식노드로 구분된다.
이진트리의 특징
- 이진트리의 모든 서브트리들도 이진트리를 이룬다. -> 재귀적 호출 용이
- 두개의 분기만 존재하므로 상대적으로 쉬운 구현 -> 균형 유지에 용이
트리 구조에서 중요한 것은 균형을 유지하는 것이다.
트리의 균형이 무너지면, 탐색·삽입·삭제 등의 연산에서 시간 복잡도가 최악의 경우 O(N)까지 증가할 수 있다.
따라서 트리의 높이를 최소화하여, 평균적으로 O(log N)의 성능을 유지하는 것이 매우 중요하다.
이진 트리는 두 개의 자식 분기(left, right)만을 가지며, 모든 서브트리 또한 동일한 구조를 따르기 때문에,
균형을 유지하기 위한 알고리즘 구현이 단순하고 일관적이다.
이러한 이유로 이진 트리는 다양한 알고리즘과 자료구조에서 널리 사용되는 기본 트리 구조로 자리잡고 있습니다.
이진트리의 종류
- 이진탐색트리
- 전이진트리
- 포화 이진트리
- 완전 이진트리
이진탐색트리

- 왼쪽 자식노드는 부모 노드의 값보다 작다.
- 오른쪽 자식노드는 부모노드의 값보다 크다.
- 중복된 값을 갖는 노드가 존재하지 않는다.
[이진탐색트리의 삽입]

크기 비교를 하며 더이상 탐색이 불가능한 위치에 삽입을 수행
[이진탐색트리의 삭제]
1. 리프노드의 삭제의 경우 -> 즉시 수행

2. 자식노드가 하나인 노드 삭제하는 경우 -> 해당 노드 삭제하고 자식노드를 부모노드 레벨로 이동
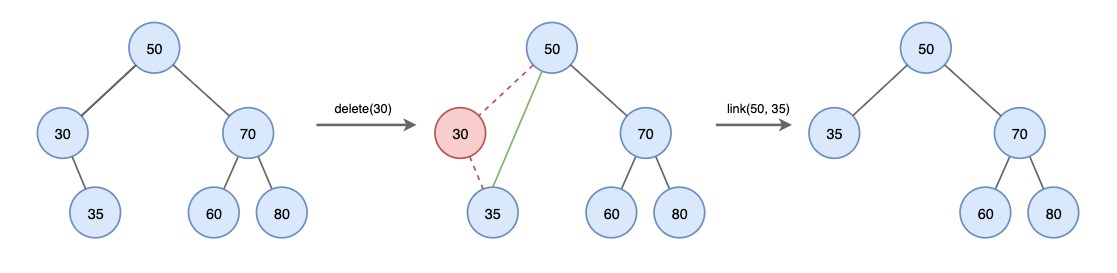
3. 자식노드가 두개인 노드 삭제하는 경우
왼쪽 노드인 경우 왼쪽 서브트리에서 가장 큰값, 오른쪽 서브트리인 경우 오른쪽 서브트리에서 가장 작은 값으로 교체

이진탐색트리의 삽입과 삭제는 위와 같이 매우 간단하고 정렬된 구조를 갖춘다는 특징이 있다.
중위순회 방식으로 탐색을 순회한다면 오름차순 정렬된 결과를 얻을 수 있다.
다만 이진탐색트리는 오름차순이나 내린차순과 같이 데이터를 정렬하여 삽입하는 경우 한쪽으로 편향된 트리구조가 발생될 수 있다.

따라서 이진탐색트리 중에서는 편향된 구조가 나오지 않고 균형을 잡기 위한 구조들이 여러개 있는데
대표적인 구조가 레드-블랙 트리와 AVL 트리가 있다.
정이진 트리(Full Binary Tree)
모든 노드가 2개의 자식을 갖거나 자식이 없는 경우를 말한다.
자식이 한 개인 경우가 없어야한다.

정이진트리는 위와 같이 리프노드의 깊이가 다를 수 있다.
포화 이진 트리 (Perfect Binary Tree)
- 모든 레벨에서 노드가 2개로 꽉 찬 트리
즉, 모든 내부 노드는 정확히 2개의 자식 노드를 가지고, 모든 리프 노드는 동일한 깊이에 있음 - 노드의 갯수 n=2^h-1

포화이진트리는 정이진트리와 비교하면 더 균형이 잘 잡힌것을 볼 수 있다.
완전 이진 트리 (Complete Binary Tree)
- 마지막 레벨을 제외한 모든 레벨의 노드가 가득 차 있음
- 마지막 레벨의 노드들은 왼쪽부터 차례로 채워져 있음
- 2^(h-1)-1 <= 노드의 수 <= 2^h-1

완전이진트리 또한 상당히 균형이 잘 잡힌 트리이다.
실무환경에서 포화이진트리를 유지한다는 것은 쉽지 않다.
데이터가 추가되면서 모든 레벨이 꽉차있는다는 것은 물리적으로 나올 수가 없기에 완전이진트리 구조가 많이 사용된다.
완전이진트리는 배열로 표현할 수 있다.
비어있는 노드가 거의 없으므로 공간을 활용도가 좋다.
완전이진트리는 균형이 잘 잡힌 트리이기에 배열로 표현시에 비어있는 공간 없이 공간을 잘 활용할 수 있다.

위와 같이 인덱스에 해당하는 값을 부모 노드로 매핑하여 완전이진트리를 표현할 수 있다.
각 배열의 인덱스는 아래와 같은 특성을 갖으며 완전이진트리를 갖는 모든 자료구조에 해당 된다.
- 노드 i의 부모노드 인덱스 : i/2
- 노드 i의 왼쪽 자식 노드 인덱스 : 2*i
- 노드 i의 오른쪽 자식 노드 인덱스 : 2*i + 1
이진트리 순회 방식 - 전위, 중위, 후위 순회
전위 순회(Pre-order)
부모노드 > 왼쪽 노드 > 오른쪽 노드
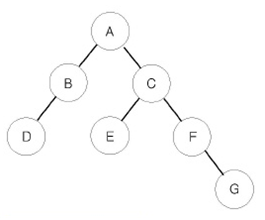
위의 트리를 전위 순회하게되면 ABDCEFG를 얻게된다.
전위 순휘는 루트노드부터 순차적으로 탐색을 수행해야하거나,
서브트리 존재시 존재하는 모든 서브트리는 우선적으로 탐색해야하는 경우 사용될 수 있다.
이로인해 전위 순회를 깊이우선순회하고도 한다.
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.left = null;
this.right = null;
}
}void preOrderTraversal(TreeNode root) {
if (root == null) return;
// 루트 노드를 방문
System.out.print(root.val + " ");
// 왼쪽 서브트리를 전위 순회
preOrderTraversal(root.left);
// 오른쪽 서브트리를 전위 순회
preOrderTraversal(root.right);
}
중위 순회(In-order)
왼쪽 노드 > 부모 노드> 오른쪽 노드
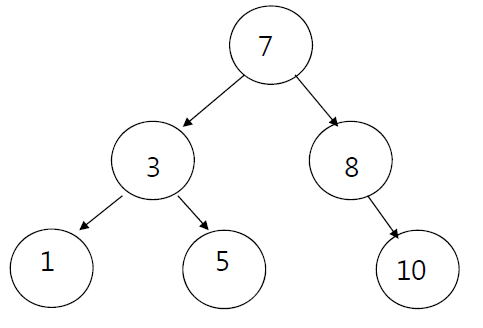
이진탐색트리를 중위순회할 경우 1-3-5-7-8-10과 같이 정렬된 결과를 얻을 수 있다.
자바의 Tree타입 자료형은 이진탐색트리를 통해 구현되는데 key 조회시 정렬된 결과를 얻을 수 있다.
void inOrderTraversal(TreeNode root) {
if (root == null) return;
// 왼쪽 서브트리를 중위 순회
inOrderTraversal(root.left);
// 루트 노드를 방문
System.out.print(root.val + " ");
// 오른쪽 서브트리를 중위 순회
inOrderTraversal(root.right);
}
후위 순회(Post-order)
왼쪽 노드 > 오른쪽 노드> 부모 노드

위 트리를 후위 순회하는 경우 1-5-3-10-8-7의 결과를 얻는다.
자식노드를 모두 방문한 후에 부모노드를 방문한다는 특징을 갖고 있다.
자식 노드의 존재여부를 모두 파악해야하는 경우 사용될 수 있다.(디렉터리, 폴더 삭제)
void postOrderTraversal(TreeNode root) {
if (root == null) return;
// 왼쪽 서브트리를 후위 순회
postOrderTraversal(root.left);
// 오른쪽 서브트리를 후위 순회
postOrderTraversal(root.right);
// 루트 노드를 방문
System.out.print(root.val + " ");
}
다진트리 - 트라이
- 문자열을 저장하고, 빠르게 탐색하기 위한 트리 형태의 자료구조
- 자동완성, 사전 검색 등에 사용됨
- 루트 노드는 비어잇는 노드
- 노드의 자손 노드는 연관된 문자열의 공통 접두사를 공유
- 자바에서 기본적으로 제공되는 자료타입이 없다.
- 문자열의 마지막 글자는 endOfWord = true로 표기하여 문자열의 종료를 나타낸다.

삽입연산

루트 노드부터 자식 노드를 탐색하여 문자열을 탐색하여 없으면 추가하고 있으면 하위 레벨 노드를 탐색을 수행한다.
문자열의 마지막 노드는 endOfWord = true로 바꿔준다.
위의 그림에서 endOfWord=true인 노드를 파란색으로 색칠했다.
삭제연산

[bus 삭제]
1. bus 탐색 후 마지막 노드로 이동
2. s의 endOfWord=true이므로 endOfWord=false로 변경
3. 자식 노드 존재하지 않으므로 삭제
4. u와 b에 대해서도 동일한 연산 수행
[appear 삭제]
1. appear 탐색 후 마지막 노드로 이동
2. r의 endOfWord=true이므로 endOfWord=false로 변경
3. 자식 노드 존재하지 않으므로 삭제
4. e에 대해 동일한 연산 수행
5. p는 자식 노드가 존재하니 삭제 불가
조회 연산
루트노드 부터 탐색하여 자식 노드를 모두 탐색하며 탐색해야할 문자열이 있는지 여부를 판단하여
존재한다면 해당 노드의 하위 노드를 다시 탐색하는 방식을 취한다.
아래 코드는 조회, 삽입, 삭제를 모두 포함한 트라이를 구현한 것이다.
import java.util.HashMap;
import java.util.Map;
public class Trie {
// Trie의 노드 정의
static class TrieNode {
Map<Character, TrieNode> children = new HashMap<>();
boolean isEndOfWord = false; // 이 노드가 단어의 끝인지 여부
}
private final TrieNode root;
public Trie() {
root = new TrieNode();
}
// 단어 삽입
public void insert(String word) {
TrieNode current = root;
for (char ch : word.toCharArray()) {
current = current.children.computeIfAbsent(ch, c -> new TrieNode());
}
current.isEndOfWord = true;
}
// 정확한 단어 검색
public boolean search(String word) {
TrieNode node = getNode(word);
return node != null && node.isEndOfWord;
}
// 특정 접두사로 시작하는 단어가 있는지 확인
public boolean startsWith(String prefix) {
return getNode(prefix) != null;
}
// 단어 또는 접두사에 해당하는 마지막 노드 반환
private TrieNode getNode(String s) {
TrieNode current = root;
for (char ch : s.toCharArray()) {
current = current.children.get(ch);
if (current == null) {
return null;
}
}
return current;
}
}
------------------------------------------------------------------------------------------------------------------
이렇게 해서 이진트리와 다진트리에 대해 알아보았다.
위에서 소개한 이진트리들은 이론적인 뼈대가 되는 자료구조이다.
실제로는 이보다 한단계 발전된 레드블랙 트리나 AVL 트리, 힙과 같은 자료구조들이 있는데,
균형을 유지하여 조회 성능을 향상시키기 위해 삽입이나 삭제와 같은 연산에 별도의 알고리즘이 추가되었다고 생각하면 된다.
해당 트리 구조는 별도의 포스팅에서 진행하겠다.
'자료구조 & 알고리즘 > 자료구조' 카테고리의 다른 글
| 이진트리와 Balanced트리의 비교 (mysql innoDB는 왜 Balanced 트리를 사용할까?) (0) | 2025.05.30 |
|---|---|
| 레드블랙트리 (0) | 2025.05.30 |
| 이진탐색트리 - AVL 트리 (0) | 2025.05.30 |
| 완전이진트리 - 힙 (0) | 2025.05.29 |
| 자료구조 개요 (0) | 2025.04.17 |
